Babies Born Slightly Under 1,500 Grams (3 Pounds 5 Ounces) Are Considered _____ Birthweight
The Birthday Problem🎈
Today'south problem goes out to a special new fellow member of the family. Welcome to the world my niece, Edison Grace Drupe! My blood brother's cute baby girl was born on his 36th altogether this past Saturday and of course this coincidence made me think of the Birthday Trouble .
So here information technology is: a special math problem for a special little girl. Someday you'll know all the math to sympathise this post (trust me, I'll brand certain of information technology!).
→ For more than math tutorials, check out Math Hacks on YouTube! ←
The Altogether Trouble in Existent Life
The offset time I heard this problem, I was sitting in a 300 level Mathematical Statistics form in a modest university in the pacific northwest. Information technology was a class of near 30 students and the professor bet that at least two of us shared the aforementioned birthday.
He then proceeded to have everyone country their birthday. When it came to my turn I stated my birthdate as "two cubed, three cubed," which made the class laugh as our cognitive professor took awhile to decipher the engagement.
Anyway like he predicted before he got to the final student a pair of matching birthdays had been establish.
So how lucky was information technology that he found a matching pair?
Warm-Up
Assumption: for the sake of simplicity we'll ignore the possibility of existence born on Feb. 29th.
Let's begin with a simple example to warm up our brains:
What is the probability that two people share the aforementioned birthday?
Person A tin be built-in on any day of the year since they're the start person we're asking. The probability of existence built-in any mean solar day of the year is 1 or more specifically: 365/365.
Since Person B must be born on the aforementioned day as Person A their probability is 1/365.
We want both of these events to happen so multiply the probabilities:
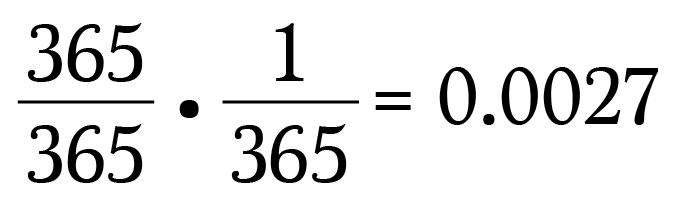
So you have a 0.27% chance of walking upwards to a stranger and discovering that their birthday is the same mean solar day every bit yours. That's pretty slim.
Merely what about a larger group?
What'south the run a risk that at least ii out of iv people share the same altogether?
Well to solve this problem nosotros'd have to summate all of the post-obit:
- Probability A and B share the same birthday
- Probability A and C share the same birthday
- Probability A and D share the same birthday
- Probability B and C share the same birthday
- Probability B and D share the same altogether
- Probability C and D share the same altogether
- Probability A, B and C share the aforementioned birthday
- Probability B, C and D share the same birthday
- Probability A, C and D share the same birthday
- Probability A, B and D share the same birthday
- Probability A, B, C and D all share the same birthday
Yuck, that's a lot of calculations! Imagine how many probabilities nosotros'd have to calculate for a classroom of thirty students!
There's gotta be a ameliorate style…
A Amend Manner: the Trick of the Complement
The simplest way of getting effectually calculating a bajillion probabilities is to look at the problem from a dissimilar angle:
What's the probability that no one shares the same birthday?
This alternate practice is helpful because it is the complete opposite of our original problem (i.due east. the complement). In probability, nosotros know that the total of all the possible outcomes (i.eastward. the sample space) is e'er equal to 1, or 100% chance.
Since the probability of at least 2 people having the same birthday and the probability of no i having the same birthday encompass all possible scenarios, we know that the sum of their probabilities is 1.
Or equivalently:
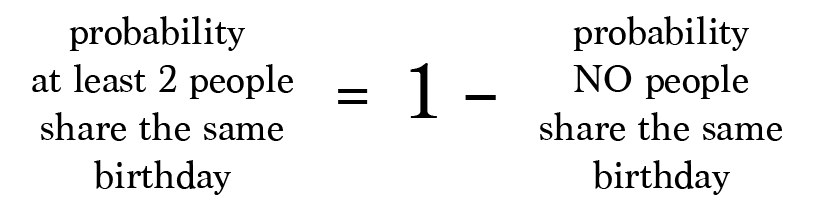
Yay! That'll be much easier to calculate.
The Calculation
Crawly! We're finally ready to detect out how safety a bet the professor made.
Let's work out the probability that no i shares the aforementioned altogether out of a room of thirty people.
Let's have this stride past pace:
- The first educatee can be born on whatever day, so we'll requite him a probability of 365/365.
- The next student is at present limited to 364 possible days, then the second student's probability is 364/365.
- The 3rd student may exist born on any of the remaining 363 days, so 363/365.
This pattern continues so that our last student has a probability of 336/365 (365 – 29 days since the students earlier her used upward 29 potential days).
Again multiply all 30 probabilities together:
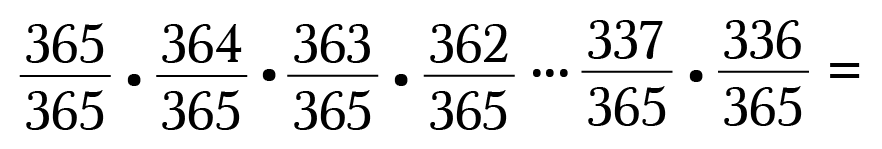
Hold upward! That's a picayune messy. Let's clean this up.
Since the denominator is thirty 365's multiplied together, we could rewrite it as:

Let'due south use factorials (symbolically: !) to further make clean this calculation up.
(Remember factorials are handy for multiplying together descending positive integers. For example 5! equals five•iv•iii•2•1 = 120.)
Using factorials, 365! would equal the production of all descending integers from 365 downward to 1. We merely want the production of the integers from 365 to 336, so we'll divide out the inapplicable numbers by dividing 365! by 335!.

Note: if this confuses y'all try a smaller value similar 5!/3! = 5•4•3•2•1 / 3•2•1. Notice how the iii•2•1 are in both the numerator and denominator. They 'cancel out' making 5!/3! = 5•4.
Putting information technology all together nosotros now accept an expression that tin exist easily entered on a scientific calculator:

This computes to 0.294 or 29.iv% chance no one in the class has the aforementioned birthday. Of course, we want the complement and then we'll subtract it from i to find the probability that at least 2 people in a group of 30 share the same twenty-four hour period of birth.

Turns out it was a pretty safety bet for our professor! He had a almost 71% take a chance that 2 or more of u.s. would share a altogether.
A Fifty-Fifty Adventure
Many people are surprised to find that if you repeat this calculation with a grouping of 23 people you'll nonetheless take a fifty% gamble that at least two people were born on the same 24-hour interval.
That's a relatively small-scale grouping of people considering that there are 365 possible birthdays! Meaning that in whatsoever group of more than 23 people it is likely that at least two people share the same day of birth.
What a crazy piddling factoid!
❤ STAY Continued ❤
Stay up-to-date with everything Math Hacks is up to!
Instagram | Facebook | Twitter
Related Reading
boatwrightanse1943.blogspot.com
Source: https://medium.com/i-math/the-birthday-problem-307f31a9ac6f
0 Response to "Babies Born Slightly Under 1,500 Grams (3 Pounds 5 Ounces) Are Considered _____ Birthweight"
Post a Comment